Info: Reference, Technology, Examples, Literature
Reference Project
LEXMED is a successfully working system for the diagnosis of appendicitis. Here the expert is a physician, the professional knowledge a set of statistical rules, the actual data is the patient's symptoms and the decision is a proposal of medical treatment provided by LEXMED.
LEXMED was tested at the Hospital 14 Nothelfer in Weingarten (Baden-Württemberg). While still experimental, it already achieves an accuracy of 88% -- not quite as good as a highly experienced surgeon, but definitely better than e.g. the average general physician.
Link: https://lexmed.hs-weingarten.de/index_e.html
Technology
1. Problem Description and Overview
When building systems for decision support we will very often be faced with
-
1.uncertain and incomplete information
(e.g. 'most birds fly' resp. it may be unknown whether a certain object X has property Y) -
2.heterogeneous information sources
(e.g. frequency data extractable from a database as well as rule knowledge obtainable from experts) -
3.resource constraints, e.g, time and cost
(e.g. 'a decision has to be taken within 30 minutes' resp. 'the cheapest solution has to be found')
Of course, in some simple cases of decision support either straightforward procedures are available or even ad hoc solutions will do. However, increasing complexity of decision support problems entails increasing demand for more general and more powerful solutions which are justified by application independent, intelligible theoretical foundations and which also allow for efficient implementation. Therefore, the problems mentioned above have been an issue of intensive research.
In order to cope with point (1) above we pursue the approach consisting of the combination of Probability Theory (ProbTh) (restricted to finite domains) and the Principle of Maximum Entropy Completion (ME) on the basis of Linear Probabilistic Constraints (LPC). We will argue in the following, that our approach is the result of a rather compelling analysis of the above mentioned challenges for decision support systems. Moreover, our approach doesn't labour under the shortcomings of most of its competitors like decision trees, score systems, fuzzy logic, Bayesian networks, neural nets, non-monotonic logics and others.
Apart from interviewing experts we use our Entropy based Data Mining Methods (EDM) to enlarge the scope of accessible knowledge (point 2).
Point (3) is taken into account by our use of Cost Matrices (CM) which translate probabilities into the financial consequences of decisions and by our efficient implementation which yields decisions within a few seconds.
For allowing user-oriented knowledge representation, on top of Linear Probabilistic Constraints an expressive knowledge representation language (HPL) was developed for the easy specification of the available information. For increasing the scope of feasible problems, methods for anticipating some of the effects of ME Completion were developed, thus allowing to modularize the completion computation. In addition, special Data structures were designed for handling large probability distributions.
Finally, we compare our technology and system to Competing Approaches and Technologies.
2. Probability Theory, Maximum Entropy and Linear Probabilistic Constraints
2.1. Probability Theory (ProbTh)
ProbTh is a fully developed and generally applicable tool for specifying uncertain and incomplete information which makes ProbTh an ideal starting point.
-
•Natural Expression of Conditional Frequency Knowledge
It is easy for most of us to express common sense knowledge by a set of 'conditional frequency expressions' (e.g. `If I think of children with symptom X, I expect them to suffer in many cases from illness Y') and to estimate the probability of some simple conclusions without difficulties (Gig96). -
•Context Sensitivity
ProbTh is a language which allows to consistently express different information in different contexts. If we specify some information in ProbTh by the most prominent form of a conditional probability, we have to specify both the 'context' for which the information holds and the information itself. With the expression 'P(b | a) = x' (or in our notation 'P(a -|> b) = x') 'a' is the context, for which the information 'P(b) = x' holds. Now 'c' may be 'true' (highly probable) in the context 'a' and in the context 'b', but 'false' (probability near 0) in the context 'a and b' or in the context 'a or b'. (See the examples under Context Sensitivity) Therefore ProbTh is a language which allows to consistently express different information in different contexts.
(An important application of this is found with Bayes Nets, which allow the specification of different kinds of dependencies for different contexts). -
•Missing Truth Functionality
But ProbTh offers even more degrees of freedom in specifying information: If we have various pieces of information in the same context, we may not know how they combine. Therefore our language has to allow different kinds of combination of evidence (which is a trivial experience in common sense, as two poisons may double their effect or may be the anti-drugs of each other. Consequently, their effect cannot be determined in general). This means that we shall not be able in general to determine a judgment - here the probability - of a compound sentence from those of its constituents. On the other side, theories which offer such a calculation, will not be able to express different situations of dependency. Example: Given the conditional probabilities 'P(a -|> b) = x' and 'P(a -|> c) = y', we cannot determine z in 'P(a -|> b * c) = z' given x and y. (See also the example ( Concerning Truth Functionality. This precludes in advance all problems with monotonic conclusions which contradict reality. This is a serious trouble spot of rule based systems which gave rise, for instance, to some nonmonotonic logics. (e.g. Lifschitz Lif89 demands such a combination rule to hold for reasoning with non-monotonic logics) As shown in (Sch96) the nonmonotonic inheritance problems given in the benchmark collection (Lif89) can be solved with ProbTh alone, while further principles (like ME below) are necessary to solve all of them. (For more information about non-monotonic logics see e.g. Mak94, Ant97 or DP96). -
•Probability as formalizing belief
Expert knowledge consists mostly of inductive experience knowledge in which experts believe to various degrees. That ProbTh is an excellent means to model belief is justified in detail in Par94. -
•Notion of Independence
ProbTh offers the notion of (conditional) independence, which has a clear information theoretic meaning even without using numbers. It allows to distinguish different kinds of information flow and prepares the ground for efficient methods of reasoning.
Traditional objections to the use of ProbTh can be overcome as follows:
-
•Objection: ProbTh is of very limited deductive power, and the amount of conclusions to be drawn is so restricted, that ProbTh alone is too weak for supporting decisions.
Refutation: The deductive power of ProbTh can be increased sufficiently by adding the principle of Maximum Entropy (see below). -
•Objection: Computations in ProbTh are impossible, as they are exponential in the number of knowledge attributes (variables).
Refutation: This criticism was refuted by Lauritzen (Lau88) who demonstrated efficient probabilistic reasoning via the use of dependency networks. (See as well `Implenentation' below on the way we compute ME.) -
•Objection: Knowledge Modelling is impossible in ProbTh, as even the expert does not know precise probabilities of his/her field.
Refutation: This objection is no more valid due to the introduction of probability intervals, which allow to represent uncertain probabilities. -
◦The objection by Kahnemann and Tversky (Kah72), (Tve74), that we are not able to reason with probability theory has been corrected by Gigerenzer (Gig96) who showed that we are well able to reason in frequencies.
-
◦(`where come the numbers from?')
Allowing the use of probability intervals - representing uncertain probabilities - refutes the objection that ProbTh obliges us to overspecify our knowledge, because it requires us to assign to our knowledge (exact) probability values for which we have no justification. -
The vague objection that ProbTh is too complicated an approach for being comprehensible to the common customer is refuted by the fact that we consider only finite domains which simplifies technical details of ProbTh - at least for the user - to undergraduates' level of knowledge. This is of great convenience for the prudent customer who wants to gain some insight into the underlying principles of the systems he relies on. Moreover, as already stated above, (Gig96) has shown, that ProbTh is well understood in terms of frequency expressions.
2.2. Maximum Entropy (ME)
In order to increase the deductive power of ProbTh to a degree which is sufficient for supporting decisions we add the (context sensitive) principle of Maximum Entropy, which reduces the remaining degrees of freedom without introducing any additional bias.
Main arguments for ME are as follows:
-
•Consistent Extension of ProbTh
-
◦Model Selection
Since ME selects one of the models provided by ProbTh on the basis of the given knowledge it is obviously consistent.
Of course, the choice of the ME-Model is context sensitive, i.e. if we change (enlarge) the set of constraints, we possibly receive a different ME-Model (for the relation to 'non-monotonic reasoning' see SF97). It also preserves the absence of truth functionality. -
◦Extension of Indifference
If there is no reason to consider two events as different, we do not want to introduce such a difference artificially and assign equal probability to the two events. This option for indifference (including a precise definition of the cases where we do not have the reason to make a difference) is respected by ME and used in PIT (see Implementation). -
◦Extension of independence
(Conditional) Independencies between parts of knowledge are extremely helpful for inferencing as they decrease context influence and this increases the number of possible conclusions to be drawn. It is therefore of particular importance that ME does not introduce new dependencies within the specified knowledge, but assumes independence where no other information is available (or, formulated sloppily, ME maximizes independence, given a set of constraints).
The Principle of Independence makes precise which kinds of independencies ME assumes, given a set of linear constraints. A subset of these independencies can be found by drawing an undirected graph, where each node corresponds to a variable and each arc between a node A and a node B corresponds to a certain constraint c, which mentions both A and B. If we interpret the resulting graph as (in)dependence map (see e.g. Pea88) (in other words, assuming the Markov property for the probability models, given the graph G) we have assumed a set of independence statements to hold for our models. Therefore, using ME means to learn the independencies from the constraints in contrast to standard methods, which assume certain independencies to hold (independently of the constraints, e.g. the more simple scoring decision systems). -
◦Minimal Information Increase
Since maximum entropy is equivalent to minimal increase of information, the ME principle chooses the most uninformative model, or most neutral model. In other words, the given knowledge is supplemented by ME in the weakest possible way. -
•Risk Minimization
As shown in (Gru00) the choice of ME-Model is strongly related to minimizing risk in bets. Since betting is quite similar to taking a decision, rooting our decisions in the ME model, means to take always the decision which is least risky. -
•Concentration Phenomenon and the Wallis Derivation
A further interesting property of the ME distribution is its that it is the center of gravity of all possible models, i.e. almost all events that satisfy certain given constraints have frequencies which are extremely close to the ME distribution. Let us take, for instance, a probability distribution to describe the relation of different kinds of balls in an urn with a fixed (but unknown) number N of balls. Consider all the 'urns', (i.e. the combination of balls of different colors), where the combination fulfills certain constraints (premises, axioms) and any combination itself generated by a random process of colouring balls. Then the most probable combinations will 'concentrate' around the ME distribution, the more we increase N. (For the formal description of the Wallis derivation see for instance (Jay95 or Sch01).) -
•Axiomatics of Information Measures
As we said above, ME chooses the most uninformative model and thus avoids the introduction of any additional bias. Trying to determine axiomatically a function which measures the amount of lack of information (uncertainty) - an attempt which goes back to Shannon's Information Theory - it can be shown that the entropy function is the only one which satisfies these axioms, i.e. it is the only one which chooses the most uninformative model (see e.g. (Jay95)).
In Prob. Reasoning we give an example for reasoning with ME compared to (monotonic) probabilistic reasoning.
2.3. Linear Constraints
For practical reasons it is important to find a type of constraints which are easy to deal with and also general enough to state all relevant expert knowledge. The ideal choice is a consistent set (conjunction) of linear (probabilistic inequality) constraints (which are linear combinations of probabilities of elementary events). The have the following nice properties:
-
•Allowing only Linear Constraints assures the existence of a unique Maximum Entropy distribution, (although more general constraints would be sufficient to assure this uniqueness.)
A unique ME model implies that every (e.g. user defined) probabilistic statement will be true or false in our model. For instance, in a medical application this would mean, that for every combination of values of possible symptoms of a patient (including the case of unknown values) the probability model yields a numerical value (i.e. not an interval) for the probability of a certain illness. -
•In addition, Linear Constraints are sufficiently general to use them as a kind of assembler language on which a very expressive High-level Probabilistic Knowledge Representation can be conceived.
-
•Finally, instead of approximating the ME distribution by general tools of non-linear optimisation, Linear Constraints have the computational advantage that the ME distribution can be efficiently computed (e.g. by directly calculating the Langrange Multiplier or by using the Newton approximation for them).
Moreover, if the set is not consistent, our algorithm tries to identify a (not necessarily unique) subset of inconsistent constraints and to inform the user how to 'repair' this set of constraints.
3. Extensions
3.1. High-level Probabilistic Language (HPL)
To express one's knowledge in the form of linear constraints is not feasible for the average expert. Therefore a HPL was designed on their basis, which permits a user-friendly specification of the available information and which is automatically translated into linear constraints. The central feature of this HPL are statements of conditional probabilities ranging over intervals, which are very useful for expressing probabilistic if-then-propositions. Especially PIT is able to handle such an expressive language (with probability intervals).
Additionally, the special type of linear constraints generated from statements of our HPL have the computational advantage that the ME distribution can be calculated without search (by directly calculating the Lagrange multiplier).
Combining Knowledge from Different Sources
While developing our application LEXMED, we found it necessary to combine knowledge from different sources, like data, experts and literature, as in most cases
-
•experts are not able to specify hundreds of rules, including complex dependencies between 3 or 4 variables, as their time is strictly limited and their dependency knowledge is not precise enough for coping with this task. Moreover, different experts often contradict themselves.
(This problem was underestimated when the first expert systems were built.) -
•Available data alone are in most cases not representative for the actual purpose and the
-
•literature often does not contain enough systematic information of the necessary precision.
As our HPL (resp. some sublanguage of it) is (close to) the output language of several datamining tools (e.g. Bayesian Nets, with some restrictions, Decision trees, some Neural nets and, of course, our own Datamining Tool) and on the other side, frequency statements are quite common in the literature (see e.g. Dom91), it is relatively easy to combine the knowledge of different sources.
This would not be so easy or even impossible, if we chose data as the basic information source. Since there are many algorithms on how to generate 'knowledge' from data (which is the topic of the large machine learning community), but (to our knowledge) there are no algorithms on how to generate justified data from 'knowledge', we have to start with the knowledge representation language and look for a datamining component which produces knowledge in our representation language.
Furthermore, constraint based systems offer a knowledge base which is easy to read, to understand, to check and to maintain. This is important, as we want to be informed about what the system knows resp. what is has learned. All this is done without making the retrieval of knowledge less efficient.
3.2. Datamining Tool
From our background in probability theory, Maximum Entropy (resp. the variant of Minimum Cross Entropy) and the concepts of independence, there is only a small step to generate corresponding datamining algorithms. These algorithms (a basic concept (multi information function) can be found in SV98) look for correlations between different attributes and construct a dependency graph, which represents the most important dependencies between the variables. This dependency graph then serves as basis for the determination of the (probabilistic) 'rules' which are necessary to build an appropriate probabilistic model (which then represents the most important dependencies of the data.) For a detailed description of this algorithm see ES99.
3.3. Cost Matrix
Basically, when asking a query, the answer of PIT will be a probability. But how are probabilities related to decisions ? Surprisingly this answer is not trivial. We have to respect different types of errors and their different costs.
In our application LEXMED it makes a difference whether we diagnose 'perforated appendicitis', where 'no appendicitis' would be correct, or we diagnose 'no appendicitis' where 'perforated appendicitis' would be correct. The latter case is of course a much bigger mistake, or in other words, much more expensive in view of the follow-up costs.
Additionally, some decisions are optimal just for uncertain cases, while others are optimal if we are (nearly) certain (see the example under Cost Matrix Structure).
We therefore use a general solution, working for any vector of faults and any vector of possible decisions with the aim to find a decision which causes minimum overall cost. Including such a cost calculation in the decision process is very simple. Let cij be the costs if the real fault is class j, but we would decide for i. Given a matrix (cij) of such (mis)classification costs and a probability pi for each real decision i, the query evaluation of PIT computes the average (mis)classification cost ACj to ACj = Sumi=1,...,n cij*pi and then selects the decision j, where ACj is minimal. This result therefore includes the uncertain knowledge (leading to probabilities for different faults) and, the different types or errors (in calculating the minimum average cost, based on these probabilities).
4. Implementational Achievements
Our implementation mainly exploits the properties of ME completion like Indifference and Independence to avoid the exponential growth of the problem size by the number of variables and constraints. These principles are used to simplify the domain (without having any influence on the outcome of the ME completion) and therefore facilitate the task of ME completion resp. augment the scope of feasible problems.
-
•Support of multivalued (textual) variables Example: P([Bloodpressure = high] * [Fever=low] ) = 0.5;
-
•Support of uncertain probabilities (Interval probabilities)
Example: P([Bloodpressure = high] -|> [Fever=low] ) = [0.2, 0.3]; -
•Internal use of the (weak and strong) principle of indifference.
Our Implementation allows to efficiently calculate and store more than a million of equivalence classes per node, each of which may contain unlimited many indifferent elementary events. -
•Using the Principle of Independence allows (in most cases) to split the calculation of the joint probability distribution into a network of smaller distributions, related by conditional independence.
The resulting datastructure is called a decomposition tree. For generating and working in such a tree see e.g. Tar85, Tru00. -
•Direct Calculation of the Lagrange Factors for Elements of our HPL.
In every iteration step of calculating the ME model, we have to adjust a current probability model to satisfy a current constraint. Therefore, it is of great importance, how fast this update can be performed. For most elements of our HPL, the necessary update is done in one step, for the remaining ones it is carried out by efficient search (Newton Algorithm). -
•Last, but not least we have developed very efficient data structures and algorithms for a fast query response. In our medical application LEXMED, we have proved that query evaluation on a knowledge base of more than 500 conditional probabilities can be done in less than a second on a standard PC.
5. Competing Technologies and Systems
Other technologies conceived for the same aims can be subdivided into three groups: Technologies based on Qualitatively Simpler Technologies, technologies which are Qualitatively Competitive, but Practically Less Handy We will shortly state our position to these technologies.
5.1. Qualitatively Simpler Technologies
-
•Score systems implicitly make strong independence assumptions between the variables. As a consequence, these systems cannot handle dependencies between different variables or different illnesses (as PIT is able to do). Technically, we can transform every Score system in a system working with PIT (but not the other way round) (see Sch00).
-
•Decision Trees also represent tools which learn from data and not from expert knowledge. Decision Trees are not applicable if certain information necessary for branching is missing and Decision Trees also require the information in a fixed order.
-
•As the well known neural networks are based on data, they do not offer a general solution for reading and combining knowledge from different sources, e.g. data bases and human experts.
-
•Derivatives of classical logic (e.g. default logic) (which work by chaining rules to infer new statements), do not fully support the necessary features of context sensitivity and missing truth functionality.
Examples of such systems and their problems can be found in Poo89, McD87. -
•As Fuzzy Logic is truth functional (i.e. it calculates the values of complex expressions by those of its parts), it cannot handle specifications as described in Example 3). Consequently, since different knowledge about dependencies cannot be expressed by using fuzzy logic, and since we expect this kind of knowledge to play an important role (as it can be expressed by frequency knowledge), we cannot use this logic for our goals.
5.2. Qualitatively Competitive, but Practically Less Handy Approaches
-
•Bayesian Networks are an advanced way of representing and retrieving uncertain knowledge, which makes extended use of probability theory. They may be based on data (and automatically learn the rules and the independence structure from data) or based on expert rules.
-
◦Bayesian Networks based on Data
For several years, a growing community works on the topic of learning Bayesian Networks from data. However, in many applications the necessary knowledge cannot be determined form data alone, and human expert knowledge must be taken into account as well. -
◦Bayesian Networks based on Expert Knowledge
If we use the Bayesian Network language for the representation of the experts' knowledge, the specification has to be complete, i.e. the expert has to fully specify the independence relationships and all the conditional probabilities of the structure, which is very likely more than the expert can provide. Here, the language of PIT offers a more general solution as it allows to specify arbitrary sets of constraints (in its language) and does not demand to specify any independence structure (see also Luk00).
No rapid prototyping:
In case of modelling expert knowledge with Bayesian Networks such knowledge has to be structured manually, which is more time consuming and costly than the automatic construction of a probability model by PIT.
No incremental update:
For the same reason, if new expert knowledge becomes available, the structure of a Bayesian Network must be manually reelaborated, while with PIT we just input the new knowledge and the update is done automatically. -
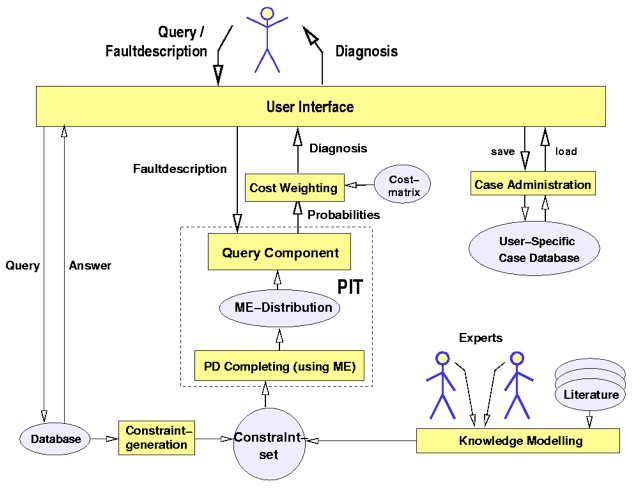
Graphical Overview of a Standard PIT Application
Examples
Sub-Sections:
Probabilistic Reasoning : example of reasoning with MaxEnt compared with classical (monotonic) reasoning.
Properties: examples concerning context sensitivity and missing truthfunctionality in probability theory.
Cost Matrix: an example for translating probabilitues into decisions (as used and described in the PIT-application LEXMED).
See image (contains tables etc which were not reformatted for the new page).
Literature
Publications and further Literature,..
-
•Some Publications of the PIT-Group (Theory, Applications (LEXMED))
-
•General Literature (Background)
-
•Links concerning Theory of Probabilistic Reasoning
-
•Links concerning Applications and Implementations of Probabilistic Reasoning
---
Publications (and technical reports) concerning PIT
-
•B. Fronhöfer, M. Schramm;
A Probability Theoretic Analysis of Score Systems.
Workshop Uncertainty in AI, Workshop at KI 2001, Vienna, Austria. FS01 -
•M. Schramm, B. Fronhöfer;
On Efficient Translations of Score Systems into Probabilistic Systems.
Workshop Uncertainty in AI, Workshop at KI 2001, Vienna, Austria. SF01 -
•M. Schramm, B. Fronhöfer;
PIT: A System for Reasoning with Probabilities.
Workshop Uncertainty in AI, Workshop at KI 2001, Vienna, Austria. SF01b -
•M. Schramm and B. Fronhöfer.
Completing Incomplete Bayesian Networks.
Workshop Conditionals, Information, and Inference Hagen, Germany, May 13-15, 2002 SF02
Springer 2004, LNCS, 3301, S.200-218;
http://dx.doi.org/10.1007/11408017_12
Informationen: http://www.springeronline.com/3-540-25332-7 -
•M.Schramm, W.Ertel, W.Rampf;
Bestimmung der Wahrscheinlichkeit einer Appendizitis mit LEXMED, Biomedical Journal, Heft 57, April 2001 (www.cms-biomedical.com) ; -
•M.Schramm, W.Ertel, W.Rampf;
Automatische Diagnose von Appendizitis mit LEXMED.
FH Ravensburg-Weingarten, Technischer Bericht, Januar 2001, 10 S SER01 -
•M.Schramm, W.Ertel, W.Rampf;
Automatische Diagnose von Appendizitis mit LEXMED.
FH Ravensburg-Weingarten, Technischer Bericht (Langfassung), April 2000; SER00 -
•P. Trunk;
Applying Graphical Models to Reasoning with Maximum Entropy
Diploma Thesis at TU Munich, Chair of Computer Science, (Guidance: M. Schramm, V. Fischer) at Prof. E. Jessen; January 2000; Tru00 -
•W.Ertel, M.Schramm; ES00
Combining Expert Knowledge and Data via Probabilistic Rules with an Application to Medical Diagnosis;
UAI 2000 Workshop on Fusion of Domain Knowledge with Data for Decision Support, Juni 2000 . Stanford CA. -
•M. Schramm;
Über das Prinzip der Minimierung der relativen Entropie.
FH Ravensburg-Weingarten,Technical Report Sch00b January 2000 -
•M.Schramm, W.Ertel; SE99
Reasoning with Probabilities and Maximum Entropy: The System PIT and its Application in LEXMED; in: K.~Inderfurth et al (ed), Operations Research Proceeedings 1999, S. 274 - 280, Springer -
•W.Ertel, M.Schramm; ES99
Combining Data and Knowledge by MaxEnt-Optimisation of Probability Distributions,
PKDD-99 (3rdEuropean Conference on Principles and Practice of Knowledge Discovery in Databases, Prag September 1999), Springer -
•M.Schramm, V. Fischer:
Probabilistic Reasoning with Maximum Entropy: The System PIT.
SF97 in Proc. of Workshop für Logikprogrammierung WLP97 -
•M. Schramm, Indifferenz, Unabhängigkeit und maximale Entropie: Eine wahrscheinlichkeitstheoretische Semantik für Nicht-Monotones Schliessen, in: Dissertationen zur Informatik, Nr. 4, CS-Press, München, 1996, (Sch96)
-
•M.Schramm, St. Schulz.
Combining Propositional Logic with Maximum Entropy Reasoning on Probability Models; ECAI '96 Workshop on Integrating Nonmonotonicity into Automated Reasoning Systems SS96 -
•V. Fischer, M. Schramm;
tabl - A Tool for efficient Compilation of probabilistic Constraints, TechReport der TU München, FS96 -
•M. Schramm, M. Greiner, Foundations: Indifference, Independence and Maxent: in.: Proc of the 14th Int. Maximum Entropy Workshop 1994, Maximum Entropy and Bayesian Methods. Kluwer Academic Publ. 1994, Ed.: J. Skilling SG95
---
General Literature
-
•Aci96
-
•Silvia Acid and Luis M. de Campos.
An algorithm for finding minimum d-separating sets in belief networks.
Technical report, Departamento de Ciencias de la Computación e I.A. Universidad de Granada, Span, 1996
http://decsai.ugr.es/pub/utai/tech_rep/acid/tr960214.ps.gz -
•Ada66
-
•E.W. Adams,
`Probability and the Logic of Conditionals', in Aspects of Inductive Logic, eds., J. Hintikka and P.Suppes, North Holland, Amsterdam, (1966). -
•Ant97
-
•G. Antoniou.
Nonmonotonic reasoning.
MIT Press, Cambridge, Massachusetts, 1997. -
•Bly72
-
•C.R. Blyth,
`On Simpson's Paradox and the Sure-Thing Principle', Journal of the American Statistical Association, 67(338), 363-381, (June 1972). -
•Bry92
-
•R.Y. Bryant,
`Symbolic Boolean Manipulation with Ordered Binary Decision Diagrams', Technical Report CMU-CS-92-160, School of Computer Science, Carnegie Mellon University, (1992).
Available at http://www.cs.cmu.edu/Web/Reports/1992.html. -
•Cen90
-
•Yair Censor, Alvaro R. Pierro, Tommy Elfing, Gabor T. Herman, and Alfredo N.Iusem.
On iterative Methods for linearly Constrained Entropy Maximization, volume 24 of Numerical Analysis and mathematical Mod.
PWN Polish Scientific Publishers, 1990. -
•CGH97
-
•Enrique Castillo, Jose Manual Gutierrez, and Ali S. Hadi.
Expert Systems and Probabilistic Network Models.
Springer Verlag, 1997. -
•Che83
-
•P. Cheeseman,
`A Method of Generalize Bayesian Probability Values for Expert Systems', in Proceedings of the 8th International Joint Conference on Artificial Intelligence (IJCAI-83), Karlsruhe, volume 1, pp. 198-202. Morgan Kaufman, (1983). -
•Cow99
-
•Robert G. Cowell, A. Philip Dawid, Steffen L. Lauritzen, and David J. Spiegelhalter.
Probabilistic Networks and Expert Systems.
Springer, 1999. -
•Dom91
-
•F.T. Dombal.
Diagnosis of Acute Abdominal Pain.
Churchill Livingstone, 1991.
erste Auflage: 1980. -
•DP96
-
•D. Dubois and H. Prade.
Non-standard theories of uncertainty in plausible reasoning.
In G. Brewka, editor, Principles of Knowledge Representation. CSLI Publications, 1996. -
•Edw95
-
•David Edwards.
Introduction to graphical Modelling.
Springer, 1995. -
•EGS95
-
•W.Ertel, C. Goller, M.Schramm, S. Schulz;
Rule Based Reasoning / Neural Nets
- Analysis Report, ESPRIT 9119 - MIX Deliverable D4.2, 1995 -
•W. Ertel and M. Schramm.
Combining Data and Knowledge by MaxEnt-Optimization of Probability Distributions.
In PKDD'99 (3rd European Conference on Principles and Practice of Knowledge Discovery in Databases), LNCS, Prague, 1999. Springer Verlag. -
•W. Ertel and M. Schramm.
Combining Expert Knowledge and Data via Probabilistic Rules with an Application to Medical Diagnosis. In UAI-2000 Workshop on Fusion of Domain Knowledge with Data for Decision Support, Stanford CA. -
•FS96
-
•(ps) (pdf) Volker Fischer and Manfred Schramm.
tabl - a Tool for Efficient Compilation of Probabilistic Constraints.
Technical Report TUM-I9636, TU München, November 1996, 38 S. -
•FS01
-
•B. Fronhöfer and M. Schramm.
A Probability Theoretic Analysis of Score Systems.
Workshop Uncertainty in AI at KI 2001, Vienna, Austria.
Technical Report of the Fernuniversität Hagen
Informatik Berichte 287 - 8/2001 (ps) (pdf) -
•Gam96
-
•Johann Gamper and Friedrich Steinmann.
Medizinische Expertensysteme - eine kritische Betrachtung.
APIS Zeitschrift für Politik, Ethik, Wissenschaftm und Kultur im Gesundheitswesen, 1996. -
•Gig95
-
•G. Gigerenzer and Ullrich Hoffrage
How to Improve Bayesian Reasoning Without Instruction: Frequency Formats
Psychological Rewiev ,102,Nr. 4,pp 684-704, 1995. -
•Gig96
-
•G. Gigerenzer.
The psychology of good judment: Frequency formats and simple algorithms.
Medical Decision Making, 1996. -
•GHK92
-
•A.J. Grove, J.Y. Halpern, and D. Koller,
`Random Worlds and Maximum Entropy', in Proceedings of the 7th Annual IEEE Symposium on Logic in Computer Science (LICS). IEEE, (1992). -
•GMP90
-
•M. Goldszmidt, P. Morris, and J. Pearl
`A Maximum Entropy Approach to Non-Monotonic Reasoning', in Proc. of the Eighth National Conference on Artificial Intelligence, Boston, pp. 646-652. AAAI, AAAI Press/MIT Press, (1990). -
•Gru98
-
•Peter Gruenwald.
The minimum description length principle and reasoning under uncertainty.
Homepage -
•Gru00
-
•Peter Gruenwald.
Maximum entropy and the glasses you are looking through.
UAI, 2000. -
•GS96
-
•(ps), (pdf), M.Greiner, M. Schramm,
A Probabilistic Stopping Criterion for the Evaluation of Benchmarks,
Technical Report, TU München, TUM-I9638, November 1996 (rev. Sep. 98) -
•GS97
-
•Charles M.Grinstead and J.Laurie Snell.
Introduction to Probability, 2nd Ed. (revised).
American Mathematical Society (AMS), 1997. -
•Hal99
-
•Joseph Y. Halpern.
A counterexample to theorems of cox and fine.
J. of Artificial Intelligence Research, 10:67-85, 1999. -
•HC73
-
•Arthur Hobson and Bin-Kang Cheng.
A comparison of the Shannon and Kullback Information Measures.
J. of Statistical Physics, 7(4):301-310, 1973. -
•HH88
-
•D.E.Heckerman and E.J.Horvitz.
The myth of modularity in rule-based systems for reasoning with uncertainty.
Uncertainty in Artificial Intelligence 2, 1988. -
•HUG
-
•Homepage of HUGIN.
http://hugin.dk. -
•Jae96
-
•Manfred Jaeger.
Representation independence of nonmonotonic inference relations.
In KR Morgan Kaufmann, San Francisco, 1996. -
•Jae97
-
•Manfred Jaeger.
Relational bayesian networks.
In UAI, 1997. -
•Jay57
-
•E.T. Jaynes.
Information Theory and Statistical Mechanics I (1957).
In R.D. Rosenkrantz, editor, E.T. Jaynes: Papers on Probability, Statistics and Statistical Physics, pages 4-16. Kluwer Academic Publishers, 1989. -
•Jay78
-
•E.T. Jaynes.
Where do we stand on Maximum Entropy?
In R.D. Rosenkrantz, editor, Papers on Probability, Statistics and Statistical Physics, pages 210-314. Kluwer Academic Publishers, 1978. -
•Jay79
-
•E.T. Jaynes.
Concentration of distributions at entropy maxima.
In Rosenkrantz, editor, Papers on Probability, Statistics and statistical Physics. D. Reidel Publishing Company, 1982. -
•Jay82
-
•E.T. Jaynes,
`On the Rationale of Maximum Entropy Methods', Proc. of the IEEE, 70(9), 939-952, (1982). -
•Jay90
-
•E.T. Jaynes.
Probability Theory as Logic.
In Paul F. Fougere, editor, Maximum Entropy and Bayesian Methods. Kluwer Academic, MIT Cambridge USA, 1990. -
•Jay95
-
•E.T. Jaynes,
`Probability Theory: The Logic of Science'.
Continually updated, fragmentary edition of approximately 700 pages available from ftp://bayes.wustl.edu//pub/jaynes, 1995. -
•Kah72
-
•Daniel Kahneman and Amos Tversky.
Subjective Probability: A Judgement of Representativeness .
Cognitive Psychology; 3, pp. 430-454, 1972. -
•Kah82
-
•Daniel Kahneman and Amos Tversky.
On the study of statistical intuitions.
Cognition; 14?, pp. 123-141, 1982. -
•Kane89
-
•Thomas B. Kane.
Maximum Entropy in Nilsson's Probabilistic Logic.
In IJCAI, volume 1, 1989. -
•Ker97a
-
•G. Kern-Isberner.
A conditional-logical approach to minimum cross-entropy,
in: Proceedings of the Annual Symposium on Theoretical Aspects of Computer Science (STACS-97), Springer 1997.
Abstract, PS, BibTeX-Entry -
•Ker97b
-
•G. Kern-Isberner.
A logically sound method for uncertain reasoning with quantified conditionals;
in: Proceedings of the International Joint Conference on Qualitative & Quantitative Practical Reasoning (ECSQARU/FAPR '97), 1997.
Abstract, PS, BibTeX-Entry -
•Ker98
-
•G. Kern-Isberner.
Characterizing the Principle of Minimum Cross-entropy within a Conditional-logical Framework.
AI, 98:169-208, 1998. -
•Ker99
-
•Gabriele Kern-Isberner.
Revising and updating probabilistic beliefs.
Frontiers in belief revision, Kluwer, pages 329-344, 1999. -
•Ker00
-
•Gabriele Kern-Isberner.
Conditional Indifference and Conditional Preservation.
In Proceedings 8th International Workshop on Nonmonotonic Reasoning (NMR'2000) , 2000. -
•KK92
-
•J. N. Kapur and H. K. Kesavan.
Entropy Optimization Prinziples with Applications.
Academic Press, Inc. , Harcourt Brace Janovich, Publishers, 1992. -
•KL99
-
•G. Kern-Isberner and T. Lukasiewicz.
Probabilistic logic programming under maximum entropy.
Technical Report 9903, Justus-Liebig Universität Gießen, 1999. -
•Lau88
-
•S. Lauritzen, D. S. (1988).
Local computations with probabilities on graphical structures and their application to expert systems.
In J. Royal Statistical Society , B, volume 50,2 of B, pages 157-224. -
•Lau96
-
•S.L. Lauritzen.
Graphical Models.
Oxford Science Publications, 1996. -
•LB82
-
•John F. Lemmer and S. W. Barth.
Efficient Minimum Information Updating for Bayesian Inferencing in Expert Systems.
AAAI,1982, p. 424-427, -
•Lem83
-
•John F. Lemmer.
Generalized Bayesian updating of incompletety specified distributions ,
Large Scale Systems 5,1983, p. 51-68, Elsevier Science, North Holland -
•Lif89
-
•V. Lifschitz, `Benchmark Problems for formal Non-Monotonic Reasoning', in Non-Monotonic Reasoning: 2nd International Workshop, ed., Reinfrank et al, volume 346 of LNAI, pp. 202-219. Springer, (1989).
-
•Luk00
-
•Th. Lukaszewicz.
Credal networks under maximum entropy.
Uncertainty in AI, pages 363-370, 2000. -
•Mal88
-
•F.M. Malvestuto.
Existence of extensions and product extensions for discrete probability distributions.
Computational Statistics and Data Analysis, ?:61-77, 1988. -
•Mal89
-
•F.M. Malvestuto.
Computing the maximum-entropy extension of given discrete probability distributions.
Computational Statistics and Data Analysis, 8:299-311, 1989. -
•Mak94
-
•D. Makinson.
General patterns in nonmonotonic reasoning.
In D.M. Gabbay, C.H. Hogger, and J.A. Robinson, editors, Handbook of Logic in Artificial Intelligence and Logic Programming, volume 3, pages 35-110. Oxford University Press, 1994. -
•McD87
-
•Drew McDermott,
A critique of pure reason
Computational Intelligence 3, p. 151-160, 1987. -
•NH90
-
•E. Neufeld and J.D. Horton,
`Conditioning on Disjunctive Knowledge: Simpson's Paradox in Default Logic', in Uncertainty in Artificial Intelligence, eds., M. Henrion, R.D. Shachter, L.N. Kanal, and J.F. Lemmer, volume 5, 117-125, Elsevier Science, (1990). -
•Nil86
-
•Nils J. Nilsson,
Probabilistic Logic,
Artificial Intelligence , 1986,28,p. 71-87 -
•Par94
-
•J.B. Paris.
The Uncertain Reasoner's Companion A Mathematical Perspective
Cambridge University Press, 1994 -
•Pea88
-
•J. Pearl.
Probabilistic Reasoning in Intelligent Systems.
Morgan Kaufmann, San Mateo, CA, 1988. -
•PIT
-
•Homepage of PIT.
http://www.pit-system.de. -
•Poo89
-
•D. Poole .
What the Lottery Paradox Tells Us about Default Reasoning
KR'89: Proc.\ of the First International Conference on Principles of Knowledge Representation and Reasoning, 1989, Kaufmann, ed.: R. J. Brachman and H. J. Levesque and R. Reiter, p. 333-340, -
•PV90
-
•J.B. Paris and A. Vencovska.
A Note on the Inevitability of Maximum Entropy.
International Journal of Approximate Reasoning, 3:183-223, 1990. -
•Qui98
-
•J.R. Quinlan.
C5.0.
www.rulequest.com. -
•Ren82
-
•A. Rényi.
Tagebuch über die Informationstheorie.
WK (Wissenschaft und Kultur) Band 34. Birkhäuser Verlag, 1982. -
•RM96
-
•W. Rödder and C.-H. Meyer.
Coherent knowledge processing at maximum entropy by spirit.
KI 96 (Dresden), 1996. -
•Sch96
-
•M. Schramm.
Indifferenz, Unabhängigkeit und maximale Entropie: Eine Wahrscheinlichkeitstheoretische Semantik für nichtmonotones Schließen.
Number 4 in Dissertationen zur Informatik. CS Press, München, 1996.
(CS-Verlag) -
•Sch00
-
•M. Schramm
Simulation von Scoresystemen durch probabilistische Systeme.
Technical Report, University of Applied Science Ravensburg-Weingarten, May 2000. -
•Sch00b
-
•M. Schramm
Über das Prinzip der Minimierung der relativen Entropie.
Technical Report, PIT-Systems, Januar 2000, submitted -
•Sch01
-
•M. Schramm
On Minimisation of Relative Entropy .
Technical Report, PIT-Systems, Jan 2001. -
•SF01
-
•M. Schramm and B. Fronhöfer.
On Efficient Decision Preserving Translations of Score Systems into Probabilistic Systems.
Workshop Uncertainty in AI at KI 2001, Vienna, Austria.
Technical Report of the Fernuniversität Hagen
Informatik Berichte 287 - 8/2001 (ps) (pdf) -
•M. Schramm and B. Fronhöfer.
PIT: A System for Reasoning with Probabilities.
Workshop Uncertainty in AI at KI 2001, Vienna. -
•M. Schramm and B. Fronhöfer.
Completing Incomplete Bayesian Networks.
Workshop Conditionals, Information, and Inference Hagen, Germany, May 13-15, 2002 -
•M. Schramm and W. Ertel
Reasoning with Probabilities and Maximum Entropy: The System PIT and its Application in LEXMED.
In SOR, Operations Research Proceedings 1999, ed.: Inderfurth K., Springer, 1999. -
•SER00
-
•M. Schramm and W. Ertel and W. Rampf
Automatische Diagnose von Appendizitis mit LEXMED (Langfassung)
FH Ravensburg-Weingarten, Technischer Bericht, April 2000; -
•SER01
-
•M. Schramm and W. Ertel and W. Rampf
Automatische Diagnose von Appendizitis mit LEXMED
Januar 2001, submitted. -
•SF97
-
•M. Schramm, V. Fischer
Probabilistic Reasoning with Maximum Entropy - The System PIT
Workshop für Logikprogrammierung 1997 , (ps) (pdf)
in Proc. WLP 97
erweiterte Zusammenfassung (deutsch) (ps) (pdf) -
•SG95
-
•M. Schramm and M. Greiner.
Foundations: Indifference, Independence & Maxent.
In J. Skilling, editor, Maximum Entropy and Bayesian Methods in Science and Engeneering (Proc. of the MaxEnt'94). Kluwer Academic Publishers, 1995.
corresponding Technical Report of the TU Munich
(ps) (pdf) -
•Sha96
-
•Glenn Shafer.
Probabilistic Expert Systems.
CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM, 1996. -
•Sha48
-
•Claude E. Shannon.
The mathematical theory of communication.
The Bell Systems Technology Journal, 27:349-423, 1948. -
•SS96
-
•
Combining Propositional Logic with Maximum Entropy Reasoning on Probability Models; ECAI '96 Workshop on Integrating Nonmonotonicity into Automated Reasoning Systems (ps) (pdf) -
•SJ80
-
•J.E. Shore and R.W. Johnson.
Axiomatic Derivation of the Principle of Maximum Entropy and the Principle of Minimum Cross Entropy.
IEEE Transactions on Information Theory, IT-26(1):26-37, 1980. -
•Ski88
-
•J. Skilling.
The Axioms of Maximum Entropy.
In G.J. Erickson and C.R. Smith, editors, Maximum Entropy and Bayesian Methods in Science and Engineereing, volume 1 - Foundations. Kluwer Academic Publishers, 1988. -
•SL88
-
•D.J. Spiegelhalter S. Lauritzen.
Local computations with probabilities on graphical structures and their application to expert systems.
In J. Royal Statistical Society , B, volume 50,2 of B, pages 157-224, 1988. -
•SPI
-
•Homepage of SPIRIT.
http://www.xspirit.de. -
•Stu89
-
•M. Studeny.
Multiinformation and the problem of characterization of conditional independence relations.
Problems of Control and Information Theory, 18(1):3-16, 1988. -
•Stu92
-
•Milan Studeny.
Conditional independence relations have no finite complete characterization.
Information Theory, Statistical Decision Functions and Random Processes. Transactions of the 11th Prague Conference vol. B, pages 377-396, 1992. -
•Stu93
-
•Milan Studeny.
Formal properties of conditional independence in different calculi of AI.
Symbolic and Quantitative Approaches to Reasoning and Uncertainty, pages 341-348, 1993. -
•Stu97
-
•Milan Studeny.
Semigraphoids and structures of probabilistic conditional independence.
Annals of Mathematics and Artificial Intelligence 21, pages 71-98, 1997. -
•SV98
-
•M. Studeny, J. Vejnarova (1998).
The multiinformation function as a tool for measuring stochastic dependence.
In Michael I. Jordan, editor, Learning in Graphical Models, pages 261-297. Kluwer Academic Publishers. -
•SW76
-
•Claude E. Shannon and Warren Weaver.
Mathematische Grundlagen der Informationstheorie.
Reihe Scienta Nova. R. Oldenburg, 1976.
Erstausgabe 1948. -
•Tar85
-
•Robert E. Tarjan.
Decomposition by clique separators.
Discrete Mathematics 55, 55:221-232, 1985. -
•Tru00
-
•P. Trunk.
Applying Graphical Models to Reasoning with Maximum Entropy.
Diplomarbeit, Lehrstuhl für Informatik VIII, Prof. E. Jessen, TU München, January 2000.
(Guidance: M. Schramm, V. Fischer) -
•Tve74
-
•Amos Tversky and Daniel Kahneman.
Judgement under Uncertainty: Heuristics and Biases.
Science 185,pp. 1124-1131, 1974. -
•Uff95
-
•Jos Uffink:
Can the maximum entropy principle be explained as a consistency requirement?
Studies in History and Philosophy of Modern Physics 26B (1995) 223-261. -
•Uff96
-
•Jos Uffink: The Constraint Rule of the Maximum Entropy Principle.
Studies in History and Philosophy of modern Physics 27, (1996) pp. 47-79. -
•Wen90
-
•W. X. Wen.
Minimum cross entropy reasoning in recursive causal networks.
In R.D. Shachter, T.S. Levitt, L.N. Kanal, and J.F. Lemmer, editors, Uncertainty in Artificial Intelligence 4, pages 105-119. Elsevier Science, 1990. -
•Wil98
-
•Jon Williamson.
The Philosophy of Diagnosis in relation to Artificial Intelligence.
PhD thesis, Kings College London, 1998. -
•Wil00
-
•Jon Williamson.
Approximating discrete probability distributions with bayesian networks.
In Proceedings of the International Conference on Artificial Intelligence in Science and Technology, 2000. -
•Whi90
-
•J. Whittaker.
Graphical Models in applied multivariate Statistics.
John Wiley, 1990.
---
Literature and links concerning Probabilistic Reasoning (Theory)
Literature (and contacts) concerning reasoning with probabilities and maximum Entropy :
-
•E. Jaynes, (died in April 1998) Probability Theory: The logic of Science
Jaynes (Ed: Rosenkrantz), Papers on Probability, Statistics and Statistical Physics -
•G. Kern-Isberner (z.B. Ker97a, Ker97b )
Lehrstuhl für praktische Informatik VIII, Fernuni Hagen, (Literaturliste Lehrstuhl) -
•Richard Jeffrey: Probabilistic Thinking
-
•E. Weydert, M. Jaeger: Max-Planck Institut für Informatik, Saarbrücken (E. Weydert)
-
•M. Jaeger: Max Planck Institute for Computer Science, Saarbrücken M. Jaeger (Homepage)
-
•Jos Uffink
z.B. Uff95 -
•See the amount of articles from J.Y. Halpern
-
•See P.C.Rhodes
-
•See P. Gruenwald for the connection between Probabilities, ME and MDL (Minimum Description Length)
Further Links concerning Entropy
Probabilities and Common Sense Reasoning
-
•Gerd Gigerenzer, Laura Martignon, Research Area "Adaptiv behavior and cognition " , Max-Plack Institut für Bildungsforschung, Berlin (Publikationen)
Probabilities and Graphs: Bayesian Networks, Learning of Bayesian Networks, etc.
-
•Learning in graphical Models; Ed.: Michael I. Jordan; Nato Science Series D, Vol. 89
-
•Building Graphical Decision Theoretic Models GeNie
-
•Construction and Inference in Bayesian Networks WEBWEAVR-III
-
•See M. Studeny
-
•See R. Greiner
-
•See Bayesian Networks
Further links of probabilistic reasoning
Uncertainty in AI: UAI
---
Literature concerning probabilistic Reasoning (Applications, Implementations)
Expert systems in Medicine:
-
•Uni Heidelberg; Prof. Wetter Knowledgebased systems in medicine (overview)
-
•Medizininformatik Weimar: Expertensysteme, Wissenbasierte Methoden
-
•K. Blekas, 1995: Medical Expert Systems
-
•KH, Uni Wien: Medizinische Experten- und Wissensbasierte Systeme
-
•P. Huber; Hat ein medizinisches Expertensystem Einfluss auf die Qualität der Ausbildung ? Ein Abstract über Erfahrungen mit ILIAD.
Related Systems
-
•An other system, working with probabilities and the principles of maximum Entropy has beed developed at the Fernuni Hagen, supervised by Prof. Rödder and Dr. Meyer (Chair for Operations Research). System SPIRIT
-
•A wellknown shell, implementing Bayesian Networks is Hugin
Further Literature (expert systems) :
-
•G. Kauermann; Literature concerning Probabilistic expert systems
-
•Cowell, Dawid, Lauritzen, Spiegelhalter: Probabilistic Networks and Expert Systems